ブログ・お知らせ
- NEWS最新の記事

【算数と数学】誕生日のパラドックス5 プログラミング思考
- 03_自由研究,06_受験関連,算数・数学,08_東京大学
「誕生日のパラドックス」最終回では、「プログラミング思考」について考えます。
第2回、第3回で、40人のクラスの中に、「同じ誕生日の人がいる確率」と「私と同じ誕生日の人がいる確率」を計算しました。
第4回では、「私と同じ誕生日の人が2人以上いる確率」を出しました。
結果だけなら、カシオさんのサイトで、自分のクラスの人数を入れると、答えを得ることが出来ます。
→ カシオ計算サイト「誕生日が一致する確率」
→ カシオ計算サイト「自分の誕生日と一致する確率」
今回は、「結果」ではなく、「計算のプロセス」もっと言えば「考え方のプロセス」を書いてきました。
「算数」「数学」というのは、数字の計算をする学問ではなく、純粋な論理学です。
だからこそ、「考え方」というのがとても大切になってくるのです。
今回、「40人のクラス」「365日」という大きな数字を扱うに際して、
「人数は4人にして「春・夏・秋・冬」の4つの季節で考える」
という手法を取りました。
数字を小さくしたケースで「パターン」を見つけ、それをもとに「式」を立てることが出来れば、あとは数字をもとに戻すことで求める答えを得られる、ということなのです。
「プログラミング思考」という言い方が最近よくされていますが、
パターン認識と、パターンへの分解、パターンの組み合わせ、
という意味では、中難度の数学の問題は、まさに「プログラミング思考」で解けるのです。
「算数」から「数学」になって感じる「難しさ」は、抽象性が高くなることから生じます。
いままで数字で表されていたものが、「x」「y」という記号で表現されることで、難度が高くなったように感じられます。
しかし、この「x」「y」によって抽象性が高くなることで、どんな時でも使えるという汎用性が高くなるのです。
苦手な人は、「x」「y」に小さな数字、分かりやすい数字を入れて考える練習をしてみましょう。
文章題も同じです。具体的な例を小さな数字で考えるようにすると、間違いを減らすことが出来ます。
例えば「植木算」の問題を考えてみましょう。
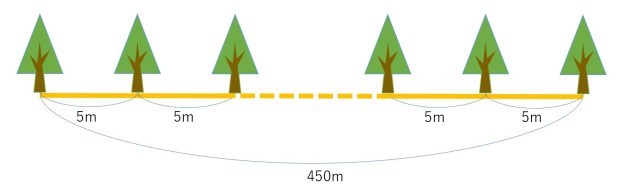
「450mの道に、5mおきに木を植える。端から端まで植えるとすると、木は何本必要か。」
450/5 = 90 という計算まではすぐに出来るでしょう。
次に端の1本を足せば良いのか、それとも2本足すのか、「90」のままで良いのか、を考えなければいけません。
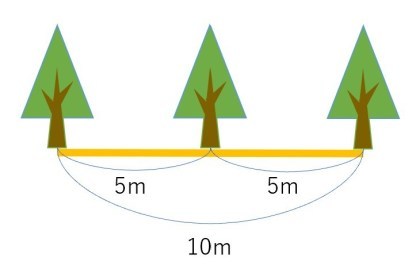
逆に言えば、端の木をどう処理するかだけの話なので、例えば10mで考えてしまえば良いのです。
10/5= 2 ですが、植えている木の本数は1本多くなっていますね。
つまり、1本足せば良い、ということが分かります。
「植木算なんて覚えてない」ではなく、実際に小さい具体的な例で考えてみれば良いのです。
簡単な例から、パターンを見抜き、式を立てて、汎用化する。
ひらめきや発想の飛躍が必要な超難問は別として、数学の基本的な問題は、この方法で考えると、答えへの道筋が見えてくることが多いです。
『思考機械の事件簿』に登場する、ヴァン・ドゥーゼン教授の決め台詞は
「2+2=4である。ときどきそうなるのではなくて、いつも必ず同じ結果をもたらす」です。
どの国でも、どの時代でも、この原則は変わりません。
そして教授は(小説の中の主人公ではありますが)
「論理的思考さえ出来れば、チェスを初めてやる人間であっても世界チャンピオンに勝てる」
と言って、本当に勝ってしまいます。
「算数」や「数学」の難問に頭を悩ましたら、「論理的思考」に立ち戻って、簡単な例からパターンを見抜いて解くようにしてみてください。
それを意識するだけで、解けなかった問題が解けるようになりますよ。
- 算数,思考機械,自由研究,数学,大学受験,誕生日のパラドックス,超難問,東京大学,論理的思考
オススメ記事
-
- お知らせ
-
- 04_イベント・講演会,08_東京大学
-
- 04_イベント・講演会,09_その他