ブログ・お知らせ
【算数と数学】誕生日のパラドックス4
- 03_自由研究,06_受験関連,算数・数学,08_東京大学
「誕生日のパラドックス」についての第4回です。
前々回、前回で、40人のクラスの中に、「同じ誕生日の人がいる確率」と「私と同じ誕生日の人がいる確率」を計算しました。
何人のクラスで何%かという結果だけなら、カシオさんのサイトで、自分のクラスの人数を入れてみてください。
→ カシオ計算サイト「誕生日が一致する確率」
→ カシオ計算サイト「自分の誕生日と一致する確率」
さて、今回がいよいよ本番。
40人のクラスの中に「私と同じ誕生日の人が2人以上いる確率」を求めてみましょう。
前回と同じく、これを考えるのに、簡単な例で考えます。
365日だと大変なので、「春・夏・秋・冬」の4つの季節で考えます。
人数も4人にしてしまいましょう。
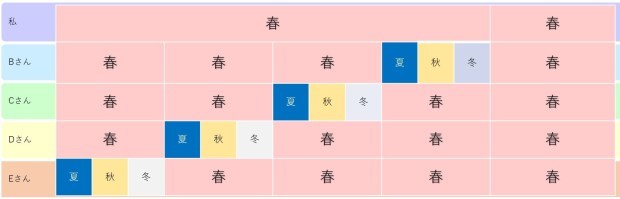
「私」の季節を「春」に決めて、「残り3人の中に、私と同じ季節生まれの人が2人以上いる確率」を求めます。
全体像を、樹形図にしてみましょう。
「私」は「春」に決めたので、「春・夏・秋・冬」のどれでも選べる他の3人について考えれば良く、
組み合わせ全体では、4×4×4 = 4の3乗 = 64 通りあります。ここまでは前回と同じです。
このうち、「3人のうちの2人あるいは3人ともが私と同じ季節(春)の生まれである」、という確率を求めるわけですが、
今回は「余事象」を考えるのが難しそうなので、場合分けして積み上げていく方法で考えてみましょう。
@)3人のうち2人が「私」と同じ季節の生まれである
B&C、C&D、B&Dの3通りがあります。
3人から2人選ぶ方法は、3C2と表現し、この計算は (3×2)/(2×1) = 3 と求められます。
今回は、3人一緒の場合は別の計算をするので、3人目は別の季節(夏か秋か冬)にしなければいけません。
なので、3×3 = 9 通り です(下の図参照)。
A)3人のうち3人が「私」と同じ季節の生まれである(全員が同じ季節(春)生まれ)
これは3人から3人選ぶ計算になります。3C3 = (3×2×1)/(3×2×1) = 1
1通りしかありません。
@)とA)の場合を足すと、9 + 1 = 10 通りの組み合わせが出来ます。
これを全体の数である64で割ると、10/64 = 0.156.. 約16%となります。
まだ少し、全体像が見えにくいですね。
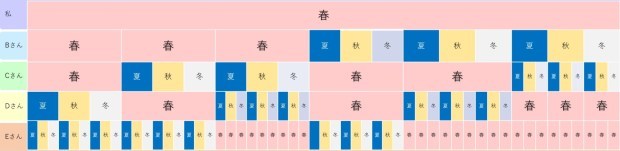
Eさんにも入ってもらって、5人の場合を考えましょう。
全体の数は、4×4×4×4 = 4の4乗 = 256 通り になります。
@) 4人のうち2人が「私」と同じ季節の生まれである
4人から2人を選ぶので、先程と同じように、4C2を計算すると、 (4×3)/(2×1) = 6 通り の組み合わせがあります。
BさんとCさんが春生まれの時、DさんとEさんは春以外の季節になります。
どの組み合わせの時も同様になるので、6×3×3 = 54 通りの組み合わせが出来ます。
A) 4人のうち3人が「私」と同じ季節の生まれである
4人から3人を選ぶので、4C3を計算すると、(4×3×2)/(3×2×1) = 4 通り の組み合わせがあります。
残り1人について春以外の季節を選ぶので、4×3 = 12 通りの組み合わせが出来ます(下図参照)。
B) 4人とも「私」と同じ季節の生まれである
4人とも同じ季節になるのは1通りだけです。
@,A,Bを合計すると、54 + 12 + 1 = 67 通りになります。
これを全体の数256で割ると、67/256 = 0.261… 約26%になります。
さぁ、考え方が見えてきました。
いよいよ本題。40人のクラスに「自分と同じ誕生日の人が2人以上いる確率」です
「4つの季節」ではなく「365日」で考えます。
人数も5人ではなく「40人」にします。
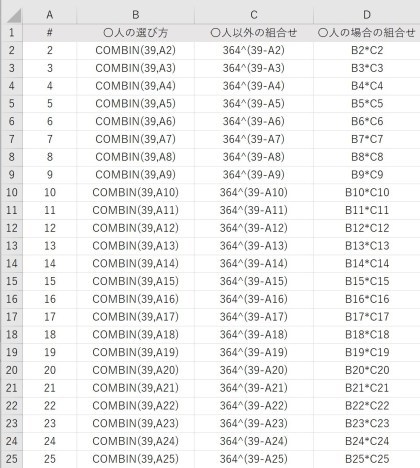
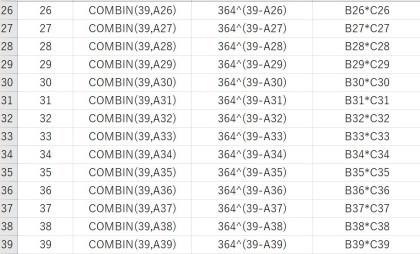
まず、全体の数は、365の39乗になります。
@) 39人(自分を除いた人数)のうち2人が「私」と同じ誕生日
2人の選び方は、39C2 = 741
この2人以外は私の誕生日以外を取るので、364(1人目)×364(2人目)×…×364(37人目) = 364の37乗
この2つを掛け合わせると、組み合わせの数が出ます。
A)39人のうち3人が「私」と同じ誕生日
3人の選び方は、39C3 で、この3人以外は 364の36乗
B)39人のうち4人が「私」と同じ誕生日
4人の選び方は、39C4 で、この4人以外は 364の35乗
そろそろ仕組みが見えてきたので、Excelを使って計算してみましょう。
「C」はcombinationの頭文字で、Excelの関数では「=COMBIN(左,右)」と表記します。
また、364の35乗は、「=364^35」と表します。
Dの列を合計すると、「40人のクラスに私と同じ誕生日の人が2人以上いるケース」の数が出てきます。
これを365の39乗で割ると、0.52%という確率が出てきます。
さすがに手計算では無理ですね…。でも、なんとか、確率を求めることが出来ました。
次回は最終回、難しい数学の問題をどう考えて解くかについてまとめましょう。
- 確率,算数,私の誕生日,自由研究,数学,大学受験,誕生日のパラドックス,東京大学,同じ誕生日の人
オススメ記事
-
- 04_イベント・講演会,08_東京大学
-
- 04_イベント・講演会,09_その他
-
- 04_イベント・講演会,理科