ブログ・お知らせ
【算数と数学】誕生日のパラドックス2
- 03_自由研究,06_受験関連,算数・数学,08_東京大学
前回、「誕生日のパラドックス」という有名な問題についてお話をしました。
40人のクラスで、クラスの中に、「私と同じ誕生日」ではなく、どのペアでもトリオでも良いので、
とにかく、「同じ誕生日の人がいる」という確率は、どれくらいだと思うか、という問題でした。
365日のいつ生まれたかはランダムなので、結構少ない確率になりそうだな、と感じるけれども、
計算すると、40人のクラスに同じ誕生日の人がいるのは、89%の確率になる、というお話でした。
何人のクラスで何%かという結果だけなら、カシオさんのサイトで、自分のクラスの人数を入れてみてください。
→ カシオ計算サイト「誕生日が一致する確率」
今回は、さて、これはどういう計算なんだろう、というお話です。
これを考えるのに、簡単な例で考えてみましょう。
365日だと大変なので、「春・夏・秋・冬」の4つの季節で考えます。
人数も4人にしてしまいましょう。
「4人の中で、同じ季節生まれの人がいる確率」を求めます。
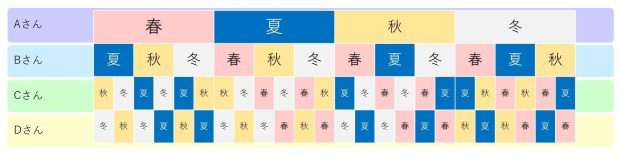
全体像を、樹形図にしてみましょう。
…全然簡単ではなかったですね(笑)
黒板で書くときは、説明しながら省略して、もっと分かりやすく図に出来るのですが…
Aさんは「春・夏・秋・冬」のどれでも選べて、Bさんも、Cさんも、Dさんも、ということになるので、
組み合わせ全体では、4×4×4×4 = 4の4乗 = 256 通りあります。
このうち、「誰か二人以上が同じ季節の生まれである」、という確率を求めるわけですが、
これを場合分けしながら何通りあるのかを考えていくと、かなり複雑になります。
こういう時に「余事象」を使います。
つまり、反対は何か、を考えて、その確率を1から引くのです。
この場合の反対は、「4人がみんなバラバラの季節生まれ」です。
「4人がみんなバラバラの季節生まれ」でなければ、誰かと誰かが同じ季節生まれになります。
もしかすると4人とも同じ季節生まれかもしれません。
では、上の図の中で、4人がバラバラの季節になる組み合わせを考えましょう。
Aさんは4通りの季節を選ぶことが出来ます。
Bさんは、Aさんの選んだ季節は選べないので、3通りのパターンがあります。
Cさんは、AさんとBさんの選んだ季節は選べないので、2通り。
Dさんは、最後に残った季節を選ぶことになります。
今度は図に収まりました。
4人全員がバラバラの組み合わせは、
4×3×2×1 = 24 通りです。
では1から24/256を引きましょう。
これを計算すると、(256-24)/256 = 0,906… となります。
つまり、4人いれば、90%の確率で、「誰か二人以上が同じ季節の生まれ」になる、ということです。
ちなみに、5人以上だと、絶対に(100%)「誰か二人以上が同じ季節の生まれ」になります。
季節は4つしかないので、4人がバラバラでも、5人目が前の誰かと一緒になってしまうのです。
これは「鳩の巣原理」という別の考え方に発展していきます。
さて、話を戻しましょう。
「4つの季節」ではなく「365日」で考えます。
人数も4人ではなく「40人」にします。
全体の数は、365×365×…×365 = 365の40乗 通りになります。
「同じ誕生日の人がいる」の反対は、「全員がバラバラの誕生日」になりますので、
先程と同じように考えると、
365(1人目)×364(2人目)×363(3人目)×…×326(40人目) = 365!/325! 通り
この数字を全体の数である365の40乗で割ると…約10.8% になります。
これを100%から引くと、今回の答えである89%が出てきます。
それにしても、高い確率に感じますね。
これは、問題を見た時に、無意識のうちに「自分と同じ誕生日の人がいる確率」を考えてしまうからだと言われています。
ちなみに、「私と同じ誕生日の人がいる確率」は、約10%。
(カシオ計算サイト「自分の誕生日と一致する確率」)
これと比べると、はるかに高い数値になりますね。
次回は、この「私と同じ誕生日の人がいる確率」を計算します。
- 確率,算数,私の誕生日,自由研究,数学,大学受験,誕生日のパラドックス,東京大学,同じ誕生日の人
オススメ記事
-
- 04_イベント・講演会,08_東京大学
-
- 04_イベント・講演会,09_その他
-
- 04_イベント・講演会,理科