キッズアース播磨町校「共明塾」

ブログ・お知らせ

【2024年4月1日】新年度スタート！～暦のお話～

    03_自由研究,算数・数学
SDGsアドバイザーが講師をつとめる、兵庫県の理科実験教室、キッズアース播磨町校です。サイエンスショーや、Youtubeでの「1分間実験動画」配信なども行っています。お気軽にお問合せください。
東大卒講師が勉強のノウハウを楽しく教える、播磨町の共明塾です。神戸、加古川、明石、高砂からも是非お越しください。

4/1、2024年の新年度は、月曜日からのスタートです。
なんだか気持ちが良いですね(笑)

では、4/1が月曜日になるのは、何年に1回くらいなのでしょうか。
曜日は月～日まで7つあるので、普通に考えると7年に1回、という事になりますが…。

「○○年から●●年までに何回あるか」とすると、中学入試にありそうな問題になります(笑)

【1年で曜日はいくつズレる？】

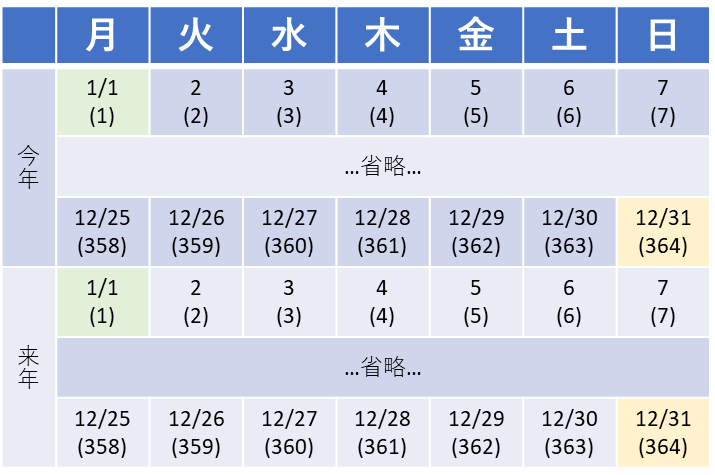
考えを整理するために、まず、365日を7で割ってみましょう。
そうすると、52余り1となります。

1年の年数が7で割り切れる（余り0の）場合、つまり1日が364日ならば、「今年の曜日」と「来年の曜日」は同じになります。



しかし、実際には1年は365日で、7で割ると1余るので、曜日が1つズレます。


なので、4/1で考えると、今年が月曜ということは、来年は火曜で、再来年は水曜…と進んで、7年後に月曜日となる、はずなのですが…。

【「うるう年」の存在】


現実の暦には、「閏年（うるうどし）」があります。
2024年はちょうど「閏年（うるうどし）」でした。 
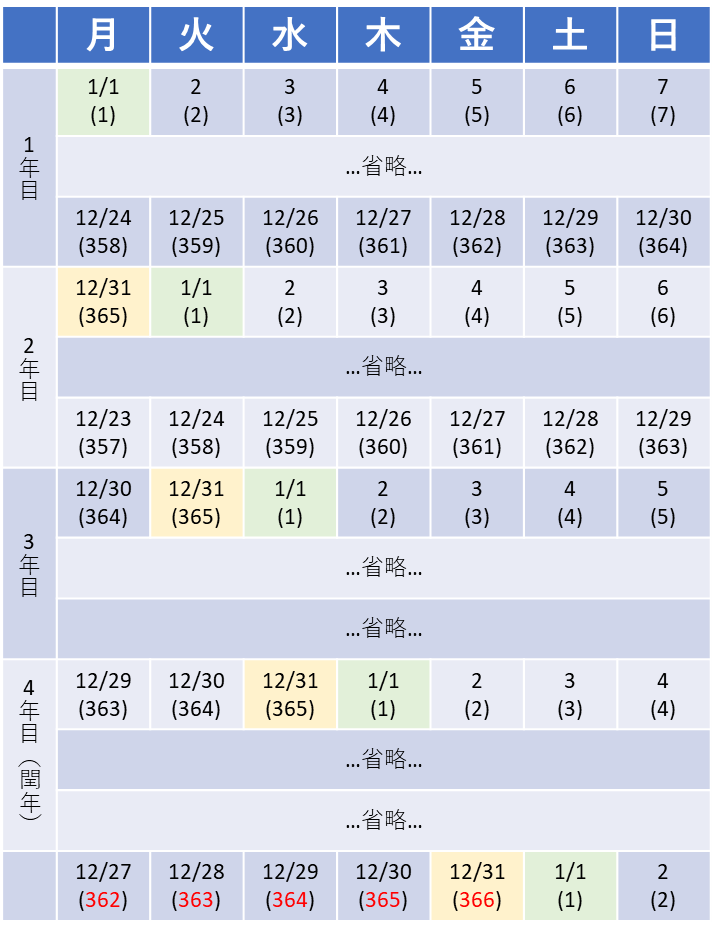
4年に1度、2/29が現れ、1年が366日になるのです。


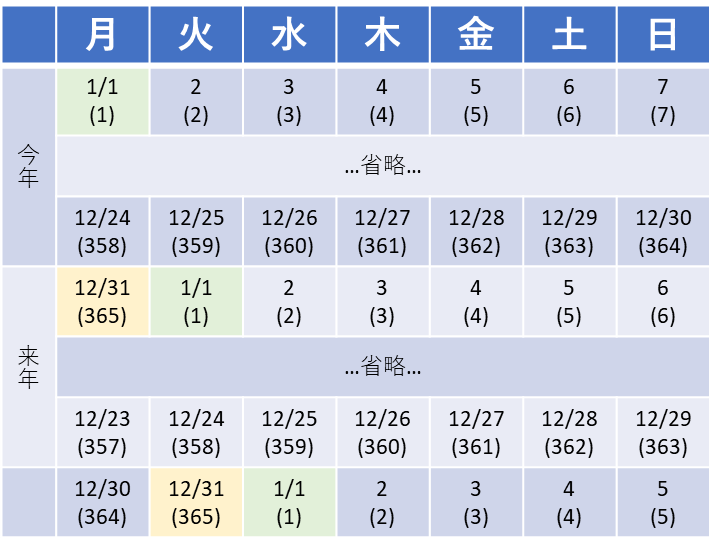
365日（余り1）で1つズレるのですから、366日（余り2）だと、2つズレることになります。
しかも増えるのは2月ですから、4月はもう影響を受けている、つまり去年のカレンダーからは2つズレている、ということになります。
たしかに、2023年の4/1は、一つズレた日曜日ではなく土曜日でした。

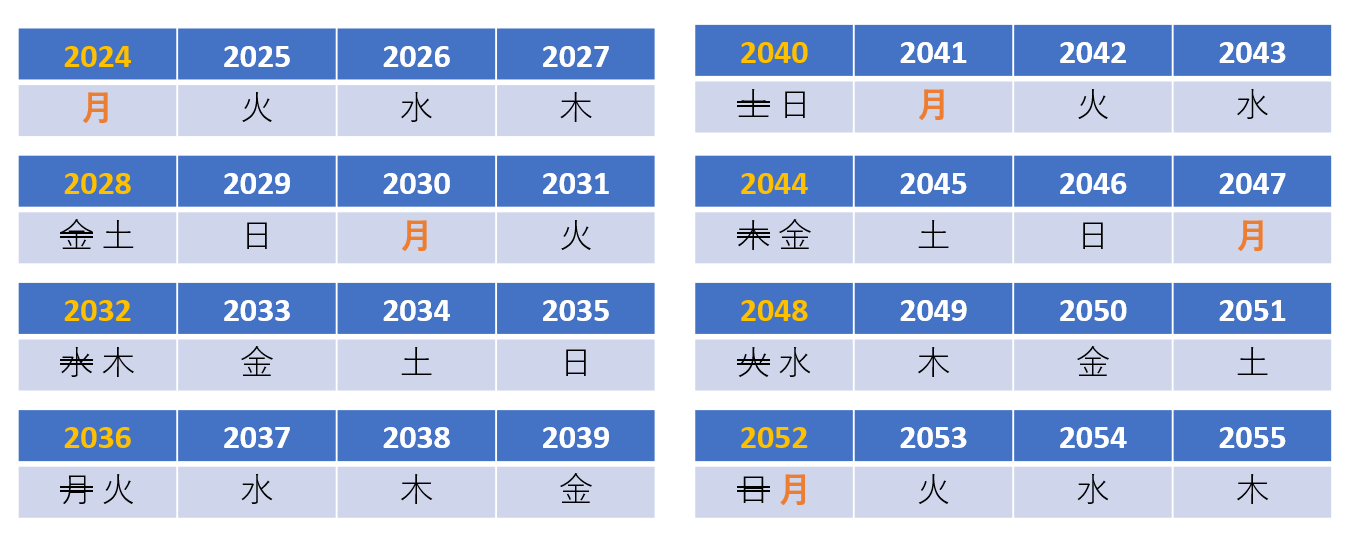
「閏年（うるうどし）」を含めて、2024年から先を表にしてみましょう。


図から分かるように、28年周期で「閏年で月曜」に戻ってきます。
この28年の間に、月曜は4回あります。

まぁ、この28という数字が、4 x 7 なので、それはそうですね、という話ですし、
最初にお話したように、割り算すれば、7年に1回、という普通の答えが出てきます。

しかし、決して7年に1度ある、というわけではなく、表を見た通り、少しランダムな感じがしますね。

例えば同じ10年にしても
「2024年～2033年」「2031年～2040年」「2036年～2045年」
では答えが違ってきます。（それぞれ、2回／0回／1回）

14年にしても（7年に1度なら2回のはずですが）、
「2024年～2037年」「2031年～2044年」「2041年～2054年」
で答えは違います。（それぞれ、2回／1回／3回）

【カレンダーの問題】

カレンダーの問題は、中学入試で計算問題として出されることがありますが、こうやって、計算問題とは違う目で眺めてみても面白いですね。

自分や友達の誕生日が何曜日だったか、というのは、調べれば簡単に出てきますけど、計算して出してみて、答え合わせする、という楽しみ方もあります。

また、万年カレンダー作成のヒントにもなりそうです。

カレンダーは周期性があるので、中学生の整数の問題などにも出てくることがあります。

あまり眺めることはないかもしれませんが、数学的な目で見てみると、違った発見があるかもしれませんよ。

※「閏年（うるうどし）」について


（1）西暦年号が4で割り切れる年をうるう年とする。
（2）（1）の例外として、西暦年号が100で割り切れて400で割り切れない年は平年とする。

例えば、西暦2004年、2008年、2012年……は（1）に当てはまりますので、うるう年になります。

また、西暦2100年、2200年、2300年は（2）に当てはまりますので、平年となります。

さらに、西暦2000年、2400年は、100でも割り切れますが400でも割り切れてしまいますので、（2）には当てはまらず、（1）のとおりにうるう年となります。

    一覧に戻る

    オススメ記事